Discovery of Electron Spin

20 May Discovery of Electron Spin

Wolfgang Pauli was born in Vienna in the same year that Max Planck introduced quantization. He was five when Einstein published his theory of relativity. At the age of 19, while a student at the University of Munich, he was asked to write an encyclopedia article on Einstein’s theory. The article was so brilliant that when Einstein read it he commented that perhaps Pauli knew more about relativity than he himself did. In 1925, five years before postulating the neutrino, Pauli introduced his Exclusion Principle. He showed that the various atomic spectra would make sense if the electron states in an atom are described by four quantum numbers and if each of these states is occupied by only one electron. In other words, once a given state is occupied, all other electrons are excluded from that state. Pauli realized that one of the numbers must represent energy, which is related to the distance from the nucleus (if we regard the states as orbits), while two other numbers represent angular momentum, which has to do with the shape and orientation of the orbit. However Pauli could find no physical significance for the fourth quantum number, which was needed empirically. The significance was found that same year by two Dutch physics students.

George Uhlenbeck and Samuel Goudsmit were studying certain details of spectral lines known as the anomalous Zeeman effect. This eventually led them to the realization that Pauli’s fourth quantum number must relate to electron spin.  Here is the story in Goudsmit’s delightful and self-effacing words – a story that conveys the groping and uncertainty that exist in the struggle to understand nature, as contrasted with the logic and certainty that are imposed after the battle is won.

The Pauli principle was published early in 1925… if I had been a good physi­cist, then I would have noticed already in May 1925 that this implied that the electron possessed spin. But I was not a good physicist and thus I did not realize this… Then Uhlenbeck appears on the scene… he asked all those questions I had never asked… When the day came that I had to tell Uhlenbeck about the Pauli principle – of course using my own quantum numbers – then he said to me: “But don’t you see what this implies? It means that there is a fourth degree of freedom for the electron. It means that the electron has a spin, that it rotates”… I asked him: “What is a degree of freedom?” In any case, when he made his remark, it was luck that I knew all these things about the spectra, and I said: “That fits precisely in our hydrogen scheme which we wrote about four weeks ago. If one now allows the electron to be magnetic with the appropriate magnetic moment, then one can understand all those com­plicated Zeeman-effects. – S. Goudsmit

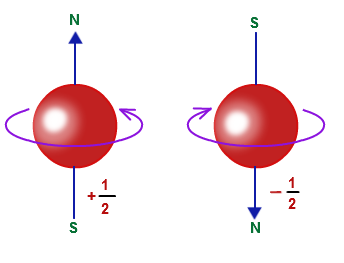
And so was introduced the idea that the electron spins on its axis (still thinking of the electron as a particle) and that this spin has a value of ½, as contrasted with the photon’s spin of 1.

The next step was to see if this idea is consistent with experiment. During a course at Harvard University, Prof. Wendell Furry gave the following account of how this happened (as best I recall):

After Uhlenbeck and Goudsmit had the idea that electron spin might explain the anomalous spectroscopic results, there remained the crucial task of determining if the effect is in the right direction. This involved the kind of calculation that all physics students have to suffer through in which polarity, direction of spin, direction of magnetic field, the “right-hand rule”, etc., get all confused and make the head spin (no pun intended). In other words, there are many opportunities to go wrong, and many do. Well, the story goes, each man did the calculation and when they compared notes they found they had opposite results. One of them had obviously made a mistake, so they went back to check their calculations. As it happened, each found an error, so they were still in disagreement. At this point they went to their mentor, Paul Ehrenfest, who happened to have a distinguished visitor named Albert Einstein. It was decided that the four of them would do the calculation independently (remember, we are talking about elementary physics here). When they got together the result was 2-2. They finally broke the deadlock by counting Einstein’s vote twice. – W. Furry (reconstructed)

I believe that this story was a joke, making fun of the difficulty physicists have in keeping track of the proper sign. (It is said that the difference between a good and a bad physicist is that the good one makes an even number of errors, so the final sign is correct.) It also pokes fun at the “papal” authority of Ein­stein, although Uhlenbeck did say that Einstein visited Leiden in 1925 and “gave us the essential hint” to complete the calculation.